Liver#
Pharmacokinetic models in DC-MRI assume that the liver consists of at most three spaces, as shown in the diagram below.
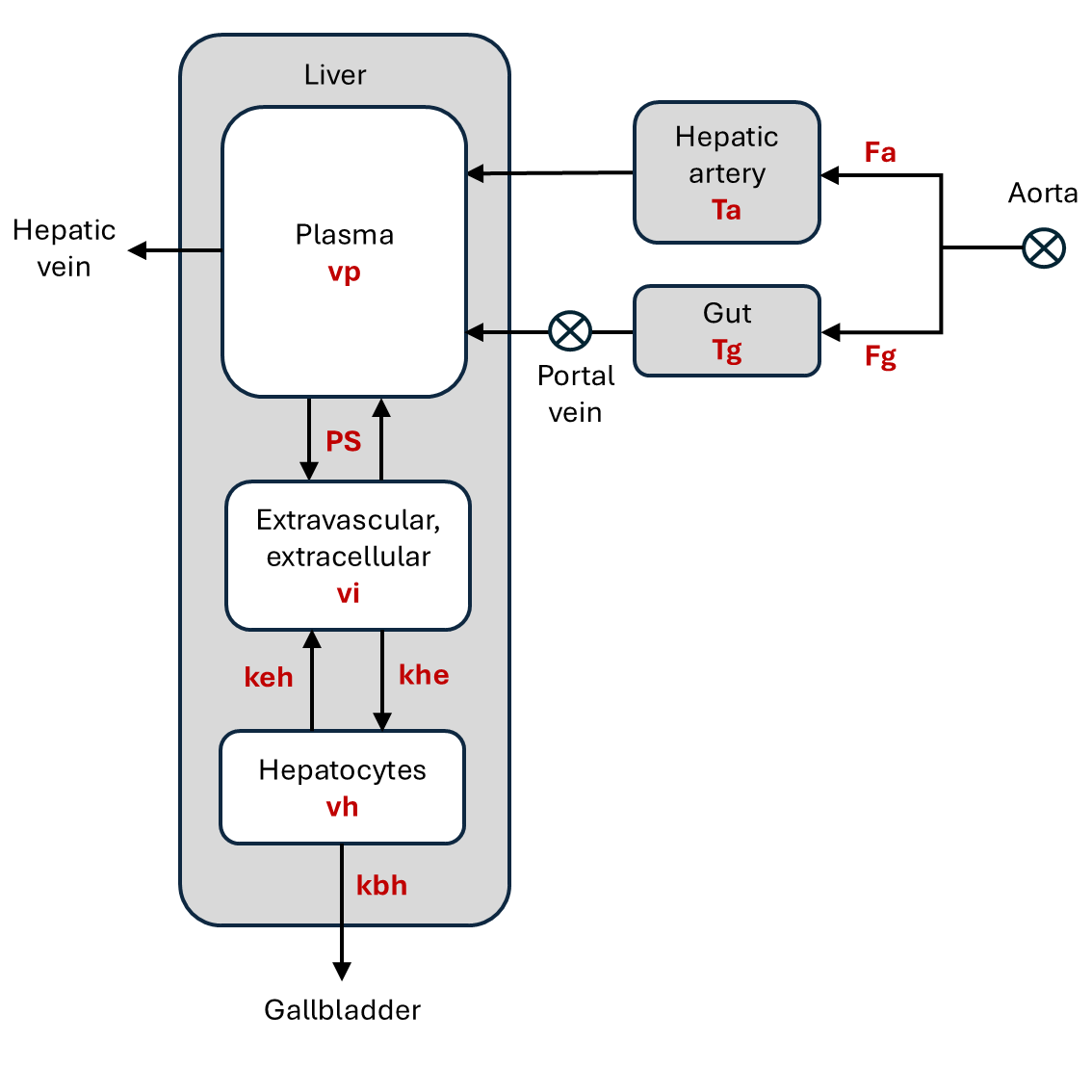
A diagram of the indicator transport into and out of the liver compartments, showing their inputs and outputs. The free model parameters are shown in red. A plasma compartment recieves inflow of plasma from the hepatic artery (Fa) and the portal vein (Fv), which collects venous blood that has passed through the gut. The plasma exchanges indicator with the liver’s interstitium with a bi-directional exchange rate (PS). The interstitium exchanges with the hepatocytes which evacuate indicator to the gall bladder. Any indicator that is not evacuated in this way will be cleared from the plasma compartment through the venous outlet.#
All models currently implemented in dcmri assume that the hepatic artery
can be modelled as a plug flow system with mean
transit time Ta. They also assume that the walls of
the liver capillaries are highly permeable to contrast agent so that plasma and
interstitium are well-mixed (\(PS\to\infty\)). Future versions will
generalize to include models with finite PS.
Definitions and notations#
Short name |
Full name |
Definition |
Units |
|---|---|---|---|
Ta |
Arterial mean transit time |
Time for blood to travel through the hepatic artery |
sec |
fa |
Arterial flow fraction |
Arterial fraction of the total blood flow into the liver |
None |
Fp |
Liver plasma flow |
Total flow of plasma into the liver tissue, per unit tissue volume. |
mL/sec/cm3 |
ve |
liver extracellular volume fraction |
Part of the liver tissue taken up by the extracellular space |
mL/cm3 |
De |
Extracellular dispersion |
Bolus broadening in the extracellular space of the liver |
None |
Te |
Extracellular mean transit time |
Average time to for an indicator molecule to travel through the liver extracellular space |
sec |
khe |
Intracellular uptake rate |
volume of extracellular fluid fully cleared of indicator per unit time and tissue |
mL/sec/cm3 |
kbh |
Biliary excretion rate |
volume of intracellular fluid fully cleared of indicator per unit time and tissue, by transport to bile |
mL/sec/cm3 |
Th |
Hepatocellular mean transit time |
Average time for an indicator molecule to travel through the hepatocytes |
sec. |
Short name |
Full name |
Parameters |
Solution |
|---|---|---|---|
Dual-inlet extracellular |
|||
2I-EC |
Dual-inlet extracellular |
ve, Fp, fa, Ta |
Eq. (4) |
2I-EC-HF |
Dual-inlet extracellular high-flow |
ve, fa, Ta |
Eq. (6) |
Single-inlet extracellular |
|||
1I-EC |
Single-inlet extracellular |
ve, Fp, fa, Ta, Tg |
Eq. (7) |
1I-EC-D |
Single-inlet extracellular dispersion |
ve, Te, De |
Eq. (8) |
Dual-inlet intracellular |
|||
2I-IC |
Dual-inlet intracellular |
ve, Fp, fa, Ta, khe, Th |
|
2I-IC-HF |
Dual-inlet intracellular high-flow |
ve, fa, Ta, khe, Th |
|
2I-IC-U |
Dual-inlet intracellular uptake |
ve, Fp, fa, Ta, khe |
|
Single-inlet intracellular |
|||
1I-IC-D |
Single-inlet intracellular dispersion |
ve, Te, De, khe, Th |
|
1I-IC-DU |
Single-inlet intracellular dispersion uptake |
ve, Te, De, khe |
Extracellular agents#
Dual inlet#
If the contrast agent is extracellular, then by definition \(k_{he}=0\) and the hepatocyte compartment plays no role in the analysis. Since we assume fast exchange of indicator across the capillary wall, the liver can then be modelled as a single extracellular compartment with volume fraction ve. A physical interpretation for the rate constant can be derived by expressing mass conservation for the compartment in terms of the extracellular concentration c_e. Since the indicator is evacuated by the total plasma flow we have:
Writing this in terms of the tissue concentration \(C_e=v_ec_e\) we get an equation as in section Compartment with mean transit time:
If a reliable concentration can be measured in the aorta (ca) and in the portal vein (cv), then:
And the solution is:
In this case the model is fully defined by the four parameters ve, Fa, Fv and Ta. An alternative parametrization uses the total plasma flow Fp and the arterial flow fraction fa:
Eq. (4) is the dual-inlet model for extracellular tracer, or 2I-EC.
If the plasma flow is very high then the bolus dispersion in the liver is not separately measureable. The extracellular space is then a simple pass:
This is the dual-inlet extracellular high-flow model, or 2I-EC-HF.
Single inlet#
If the acquisition is not optimized for data collection in the portal vein, then a portal-venous concentration may not be available. In theory this can be addressed by modelling the passage through the gut. If we model the gut as a compartment then Eq. (4) becomes:
This is a single-inlet extracellular model (1I-EC). If the dispersion in liver and gut cannot be separated, an alternative approach is to simplify the model by considering the extracellular space of liver and gut as a single combined space, and model it for instance as a plug-flow compartment: with mean transit time Te and dispersion De. Using the propagator \(h\) of a plug-flow compartment the solution is a 3-parameter model:
This is the single-inlet extracellular dispersion model (1I-EC-D). Out of the 3 parameters, only the extracellular volume \(v_e\) is a liver characteristic. The other two (\(T_e\) and \(D_e\)) are determined by the properties of the gut and the liver. In particular the blood flow into the liver is not measureable under these conditions.
Intracellular agents#
For contrast agents that enter the hepatocytes, the models must be extended with a hepatocyte compartment. In the case where backflux from hepatocytes is negligible (\(k_{hb}=0\)) this is a straightforward extension of the models for extracellular agents. The hepatocytes are modelled as a compartment (see Compartment) and an interpretation of the rate constants can be found from the conservation of indicator mass in terms of the concentration \(c_h\):
Expressing this in terms of the tissue concentration \(C_h\) we find the mean transit time of the hepatocytes:
Since there is no backflux into the extracellular space, the solution for \(c_e\) can be used as an input function to the hepatocellular compartment:
When acquisition times are short, the excretion from the hepatocytes is negligible and the hepatocytes are modelled as a trap with uptake only:
The total tissue concentration is \(C=C_e+C_h\). The intracellular models 2I-IC, 2I-IC-HF, 2I-IC-U, 1I-IC-D and 1I-IC-DU are direct extensions of the extracellular models, with the additional parameters \(k_{he}\) and \(T_h\) (see table Kinetic models for the liver).
Passage through the hepatocytes is a slow process, especially when the excretion rate is substantially impaired by disease or drugs. Measuring excretion rates reliably under such conditions is challenging and requires very long acquisition times (hours). Under those conditions the actual state of the liver may change during the acquisition, requiring a non-stationary model for the hepatocyte compartment. In the simplest scenario this can be modelled by interpolating linearly between initial values for the parameters \(k_{he, i}\) and \(T_{h, i}\) and final values \(k_{he, f}\) and \(T_{h, f}\).
