dcmri.Mz_spgr#

dcmri.Mz_spgr(R1, T, TR, FA, v=1, Fw=0, j=None, n0=0, me=1)[source]#

Longitudinal tissue magnetization of a spoiled gradient-echo sequence.

See section Longitudinal relaxation for more detail.

Parameters:

  • R1 (array-like) – Longitudinal relaxation rates in 1/sec. For a tissue with n compartments, the first dimension of R1 must be n. For a single compartment, R1 can be scalar or a 1D time-array.

  • T (float) – time since the first rf-pulse.

  • TR (float) – repetition time between rf-pulses.

  • FA (float) – flip angle of the rf-pulse.

  • v (array-like, optional) – volume fractions of the compartments. For a one-compartment tissue this is a scalar - otherwise it is an array with one value for each compartment. Defaults to 1.

  • Fw (array-like, optional) – Water flow between the compartments and to the environment, in units of mL/sec/cm3. Generally Fw must be a nxn array, where n is the number of compartments, and the off-diagonal elements Fw[j,i] are the permeability for water moving from compartment i into j. The diagonal elements Fw[i,i] quantify the flow of water from compartment i to outside. For a closed system with equal permeabilities between all compartments, a scalar value for Fw can be provided. Defaults to 0.

  • j (array-like, optional) – normalized tissue magnetization flux. j has to have the same shape as R1. Defaults to None.

  • n0 (array-like, optional) – initial relative magnetization at T=0. If this is a scalar, all compartments are assumed to have the same initial magnetization. Defaults to 0.

  • me (array-like, optional) – equilibrium magnetization of the tissue compartments. If a scalar value is provided, all compartments are assumed to have the same equilibrium magnetization. Defaults to 1.

Returns:

Tissue magnetization in the compartments after a time T.

Return type:

np.ndarray

Example

Compare SPGR tissue magnetization of a two-compartment tissue after inversion against free recovery and steady-state:

Import packages:

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> import dcmri as dc

Define constants:

>>> FA, TR = 12, 0.005
>>> TI = np.linspace(0,3,100)
>>> R1 = [1, 0.5]
>>> v = [0.3, 0.7]
>>> f, PS = 0.5, 0.1
>>> Fw = [[f, PS], [PS, 0]]

Compute magnetization:

>>> Mspgr = dc.Mz_spgr(R1, TI, TR, FA, v, Fw, j=[f, 0], n0=-1)
>>> Mfree = dc.Mz_free(R1, TI, v, Fw, j=[f, 0], n0=-1)
>>> Mss = dc.Mz_ss(R1, TR, FA, v, Fw, j=[f, 0])

Plot the results for the peripheral compartment:

>>> c = 1
>>> plt.title('Peripheral compartment')
>>> plt.plot(TI, Mfree[c,:], label='Free', linewidth=3)
>>> plt.plot(TI, v[c]+0*TI, label='Equilibrium', linewidth=3)
>>> plt.plot(TI, Mspgr[c,:], label='SPGR', linewidth=3)
>>> plt.plot(TI, Mss[c]+0*TI, label='Steady-state', linewidth=3)
>>> plt.xlabel('Time since start of pulse sequence (sec)')
>>> plt.ylabel('Tissue magnetization (A/cm/cm3)')
>>> plt.legend()
>>> plt.show()

(Source code, png, hires.png, pdf)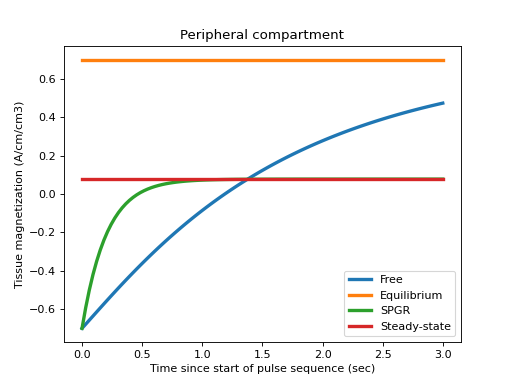

../../_images/dcmri-Mz_spgr-1_00_00.png

This verifies that the free recovery magnetization goes to equilibrium, and that the SPGR magnetization relaxes to the steady state at a shorter time than the free recovery.